Konspirationen mot eleverna

När Ola träffade Linda på en kompetensutveckling, som Ola anordnade och Linda deltog i, tänkte han: Det där är ingen vanlig lärarinna! Kanske var det fårpälsvästen, kanske var det påståendet att hennes elever minsann glatt läste populärvetenskapliga böcker om matematik helt frivilligt. Men mest troligt är att det var hennes tröttsamma framhärdande att proportionella resonemang är det viktigaste i hela grundskolan. Typiskt att folk tycker att just deras grejer är så himla intressanta, tänkte Ola och kategoriserade Linda som en galen proportionalitetskvinna. Men hon var rolig och snabbtänkt och väldigt entusiastisk, så det var värt att ta reda på lite mer om Lindas övertygelser. Efter lite samtal drog sig Ola till minnes en artikel han reviewade något år tidigare. Författaren insisterade på att proportionalitet minsann var det viktigaste begreppet i hela skolmatematiken. Hmm, sådär skriver alla om sina favoritbegrepp, tänkte Ola även då, och refuserade det hela. Var det möjligen samma galna proportionalitetskvinna? Ja, visade det sig.  (Artikeln är numera publicerad så allt är förlåtet.)

Men trägen vinner. Ni som läste vår senaste bloggpost har kanske redan anat att Ola är omvänd. Och på Biennalen i Karlstad för några veckor sedan stod Ola glatt och föreläste om proportionalitetsbegreppets förträfflighet. Två gånger till och med! För förskoleklass till sexan och för sjuan till gymnasiet. Båda gångerna tillsammans med Linda, som nu helt har frälst Ola som numera får betraktas som en fullfjädrad proportionalitets-förespråkare.

Vad är då en proportion? För att förklara det måste vi först förstå begreppet förhållande. Det går som bekant inte att förklara något begrepp utan förståelse för andra begrepp. Ett förhållande är en multiplikativ relation mellan två kvantiteter (eller två saker som Ola brukar säga, oprecis som han är). Ett sätt att uttrycka ett förhållande är \frac{a}{b}. Som ett bråk. En proportion är en likhet mellan två förhållanden. \frac{a}{b}=\frac{c}{d}. Men när vi betraktar proportioner är vi inte nödvändigtvis ute efter att beräkna kvoten hos dessa två bråk, utan fokuserar på just det faktum att de två förhållandena är lika.

Proportionella resonemang kan introduceras minst lika tidigt som man introducerar multiplikation. Betrakta följande: 

 

Ur äppelrelationen kan man dra slutsatsen att Stora Björn har 3 ggr så mycket av allt (gröna pilen). Men det följer också att eftersom Lilla björn har 4 ggr så många äpplen som apelsiner så måste detta även gäller för Stora björn (svarta pilarna). Drar vi alla dylika resonemang till sin spets och även (i enlighet med en av våra tidigare bloggposter) beaktar inverser kan vi schematisera det hela så här:

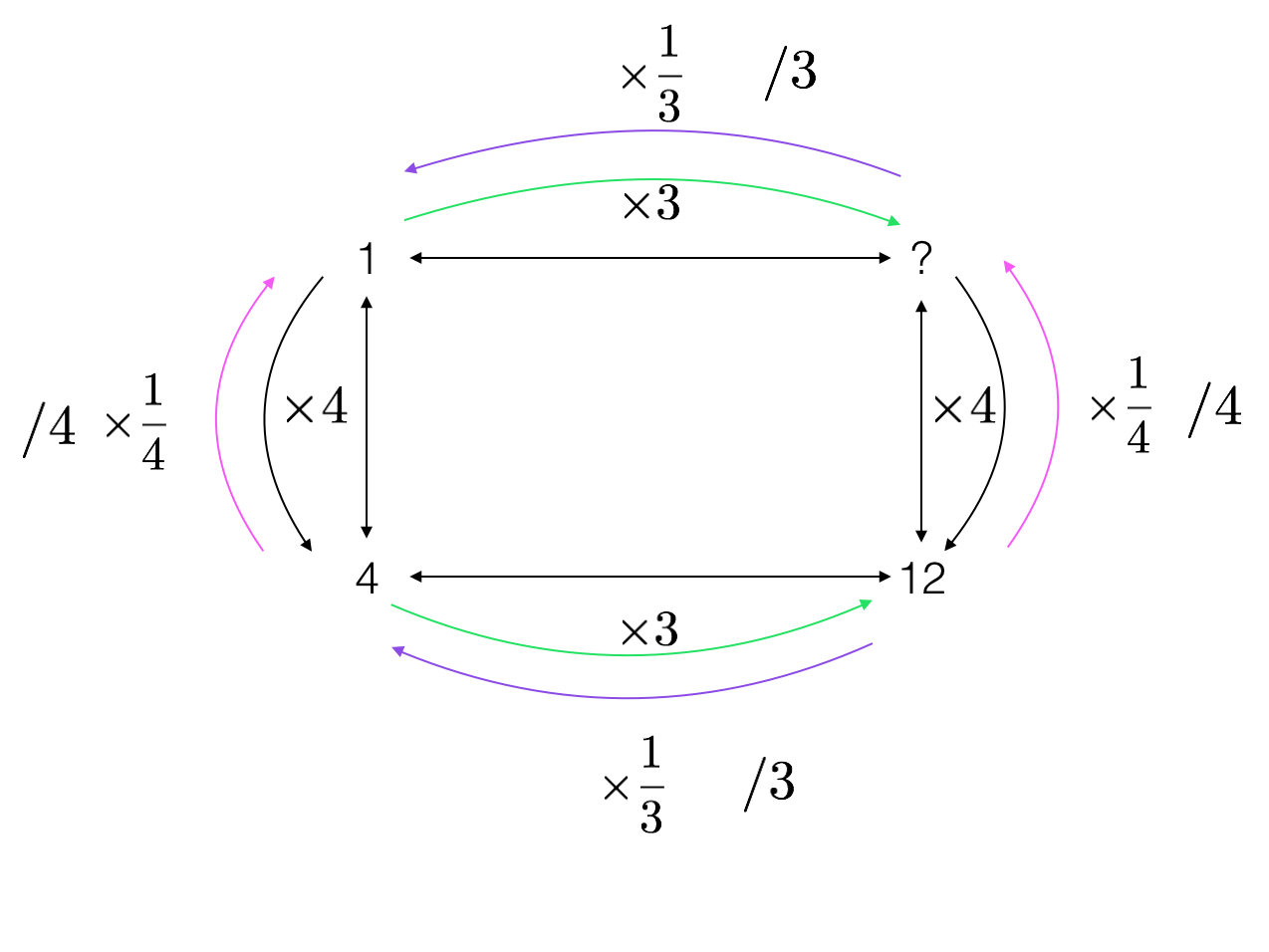
Notera speciellt att man kan tänka på inversen till multiplikation med 3 på två sätt: division med 3 eller multiplikation med ⅓. Man får massor med olika möjligheter att räkna ut vilket tal som ska stå på frågetecknets plats. Och den typ av resonemang som man för är helt oberoende av överväganden som har med den ursprungliga situationens konkreta gestaltning att göra. Det är bara det faktum att det handlar om ett proportionellt resonemang som spelar roll. Och egentligen finns förstås alla dessa relationer redan i representationen

\frac{1}{4}=\frac{?}{12}

Det är just det här som gör proportionella resonemang så förträffliga. Om eleverna lär sig att identifiera situationer där två förhållanden är lika och resonera om de inbördes multiplikativa relationerna så behöver de inte nöta in en herrans massa olika situationer i olika områden år ut och år in. Vad pratar vi om egentligen? Jo att skala upp och ner bråk, beräkna skala, procent, likformighet, sammansatta enheter som hastighet, densitet och kilopris, likformighet inom geometrin, likformig sannolikhet och alla uppgifter som illustrerar ett multiplikativt samband där tre värden är givna och det fjärde saknas beräknas enklast med just proportionella resonemang. Alla dessa funktioner som kan beskrivas som en proportionalitet f(x)=kx, U=RI, s=vt, O=\pi d…

Eleverna kan lätt få en känsla av att matematiska situationer från olika delar av skolmatematiken är fundamentalt olika, men så är det ju inte. Det är en stor befrielse för eleverna att inse att samma resonemang fungerar inom alla möjliga områden. Matematiken krymper och det är möjligt att göra en syntes på grund av denna  matematiska ide dyker upp om och om igen, inom en mängd olika områden. Titta på uppgifterna nedan. De är alla hämtade från olika kapitel i en och samma textbok för … ja fundera på när eleverna arbetar med den här matematiken och gissa?

Vikterna mellan två paket förhåller sig som 2:5. Om det ena paketet väger 10 kg, vad kan då det andra paketet väga?

Jannes hår växer 17 µm per timme. Hur lång tid tar det för hans hår att växa 4 cm?

Lös ekvationen:\frac{18}{6x}=\frac{9}{3}

Hur stor diameter har en cirkel med omkretsen 35 cm?

En skobutik säljer sina skor för 160 % av inköpspriset. Vad är inköpspriset för ett par skor som kostar 760 kr?

Fem meter rep kostar 150 kr. Vad kostar tjugo meter rep?

Under en dag gör en maskin 5900 lampor. Vid en kontroll visar det sig att 26 av dem är felaktiga. Ungefär hur många trasiga lampor borde det finnas vid en leverans av 2000 lampor?

Till 5 liter vit färg krävs det 7 droppar pigment för att färgen ska bli ljusblå. Hur många droppar pigment går det åt till 12 liter färg?

En 22 cm lång kändisdocka är tillverkad i skala 1:8. Hur lång var personen som stod modell för dockan?

En kon med höjden 16 cm har en volym på 54 cm³. Hur stor volym har en (likformig) kon med höjden 8 cm?

[Den här är något mer intrikat då eleverna behöver identifiera att radien är proportionell mot höjden och samtidigt hålla reda på att areaskalan är längdskalan i kvadrat. En lösning baserad på proportionella resonemang presenteras sist i inlägget.]

Lindas elever i Kriminalvården får träna på att identifiera om det finns ett proportionellt samband i spel i de uppgifter de ska lösa. De är ju vuxna nu och för de allra flesta har det gått sisådär med skolmatematiken, av olika anledningar. Påfallande många tycker ända att det är konstigt att ingen har gjort sig besväret att upplysa dem om att samma resonemang är tillämpligt på så många olika situationer. Det hade ju varit så mycket enklare då, att hålla reda på allt. Det är ju inte konstigt att de misstänker att de har blivit utsatta för en konspiration med syftet att får dem att känna sig korkade helt i onödan!

Ta det här med procent till exempel. Varje år sedan årskurs 5 har eleverna nött igenom ett kapitel om procent. Procent, procent, procent, procent, procent, procent. Ständigt dessa procent. Som om det skulle behövas särskild träning för att hantera ett proportionellt multiplikativt samband där vi utgår från en helheten 100?

Höjning med 20%:  \frac{600kr}{100\%}=\frac{?}{120\%}

Sänkning med 30%:  \frac{600kr}{100\%}=\frac{?}{70\%}

Eller kanske vad motsvarar delen 30 % i pengar? \frac{600kr}{100\%}=\frac{?}{30\%}

Det coola med det här tankesättet är att det egentligen inte spelar någon roll vad man sätter som täljare och nämnare, bara man är konsekvent. Det är enbart den multiplikativa relationen som spelar roll.

Problemet är kanske att procent ofta undervisas som en additiv situation där eleverna först ska räkna ut sänkningen, eller höjningen, och sen lägga till eller dra ifrån. Helt onödigt om du frågar oss. Varför inte bara servera definitionen från 1878 års ”Lärobok i Räknekonsten” av P.J. Pihlstrand. Regula de tri är en beräkningsteknik för proportionalitet, kan man säga.

Det är allt.

Kanske tycker en del att vårt resonemang verkar lite esoteriskt och abstrakt och att det inte skulle gynna förståelsen. Men de har fel. Såväl lata och ointresserade elever som genuint intresserade attraheras av tanken att attackera uppgifter från diverse områden med samma verktyg. (Observera att det inte ligger någon värdering i begreppet lat och ointresserad. Linda är rätt lat själv och att hata matematik måste betraktas som en mänsklig rättighet.) Att resonera proportionellt är inte en algoritm som kan tillämpas utan att ha sorterat informationen i uppgifterna. Som elev måste du fundera på vad som förhåller sig proportionellt till vad innan hen kan beskriva proportionen i symboler. Om inte det är bra matematiskt tänkande, då vet vi inte vad vi ska ägna oss år på lektionerna.

Här är vårt bästa tips! Hylla likhetstecknets betydelse, som är helt centralt för de proportionella resonemangen. Arbeta för att etablera en sociomatematisk norm som innebär att närhelst proportionella resonemang är tillämpliga så är det den sortens resonemang som smäller högst när det gäller att delta i klassrumsdiskursen. Då kan du krympa matematiken och bryta dig loss från oppgavediskursen. När färre uppgifter behöver räknas frigörs tid för både elever och lärare att fördjupa sina betraktelser över vad det är för sorts matematiska ideer vi arbetar med. Du och dina elever slipper också att tröska igenom ett snarlikt procentkapitel från årskurs 5 till kurs 1 på gymnasiet och bäst av allt: Dina elever får ett verktyg som hjälper den att både förstå och hantera stora delar av skolmatematiken.

Det finns mycket mer att säga om det här… men eftersom våra bloggposter tenderar att likna romaner så slutar vi här. Vi hade som mål att den här skulle bli rätt kort. Se hur det gick med den saken:-) Om du vill läsa mer så rekommenderar vi vår artikelserie om proportionella resonemang i Nämnaren nr 2,3 och 4 2017 och nr 1 2018.

P.S. För de som tycker att vi verkar vara galna proportionalitets-människor så kan vi beta med att vi räknade igenom ett NP för årskurs 9 och konstaterade att 70% av uppgifterna kunde lösas med resonemang om förhållanden och proportioner.

Angående konens volym: Eftersom höjden är proportionell mot radien så kommer radien i den mindre konen vara halva radien i förhållande till den stora. Eleverna behöver också inse att \pi/3 är en konstant i volymberäkningen.

\frac{54cm^3}{r^2\cdot 16cm}=\frac{?}{((1/2)r)^2\cdot 8cm}

En halv i kvadrat är en fjärdedel och radien annulleras vilket betyder att den nya relationen i volymberäkningen är 1/4 \cdot 8=2. De som har arbetat med skalning mellan längd, area och volym inser detta helt utan beräkningar och kan genast sätta upp nedanstående proportion:-)

\frac{54}{16}=\frac{?}{2}

dvs V=54/8=6.25 kubikcentimeter. 

 

Linda Marie Ahl & Ola Helenius