Upprepad addition är en vanlig modell för multiplikation. Det är den modell som sedan 1786 sämst har klarat sin uppgift. Eller ja, det där drog vi ju bara till med för att hamna i gott akademiskt sällskap. I själva verket vet vi inte om det på den tiden fanns någon sämre modell. Men om ni läser vidare ska ni få se en bättre från 1878.

Vi menar att multiplikation och dess egenskaper missrepresenteras med modellen upprepad addition. Multiplikationen som fenomen och dess egenskaper behandlas lättvindigt med tanke på hur stor del av den obligatoriska skolans matematik som faktiskt handlar om multiplikativa strukturer och proportionella resonemang. Vi ska argumentera för att vi borde sluta upp med det här.

Upprepad addition är en modell för multiplikation som bara gäller för naturliga tal. Med den här modellen är det t ex en helt självklar sanning all multiplikation alltid gör större (eller lika om man multiplicerar med ett). Den här uppfattningen får vi sedan ägna resten av elevernas skolgång till att försöka ta ur dem. Senast igår ställde den till problem när en av Lindas (vuxna) studenter skulle beräkna hur många frön man måste så för att få 20 livsdugliga solrosor, om grobarheten är 83%. Han hade nedtecknat en divisionsprocedur, men sedan stannade han upp i sin beräkning. Linda såg att han tvekade. -Vad är det som stör dig, frågade Linda? -Ja, det känns ju helt fel att dividera när jag vill att det ska bli fler frön… Han tyckte alltså att det var direkt obehagligt att behöva dividera med 0.85. Han lider helt klart av multiplikation som upprepad addition-villfarelsen: Division gör mindre, multiplikation gör större.

Upprepad addition är en oduglig modell för att illustrera den viktiga egenskapen kommutativitet. Att 2+2+2 är lika 3+3 kan vi ju se för att båda är lika med 6. Lika lätt är det i varje konkret fall. Men hur blir det i det allmänna fallet? Varför är a stycken b lika med b stycken a? Fundera på det du. Och hur fungerar additionsmodellen för 1/2\cdot3/5? Inte alls bra, eller hur.

Mängden forskning som påvisar problem med “multiplikation som upprepad addition” är omfattande. Ett aktuellt svenskt exempel är t ex Kerstin Larssons avhandling från 2017 och ett mer klassisk exempel är Fischbein och kollegors studie från 1985. I båda fallen visas att den additionsbaserade modellen leder till problem för elevernas uppfattning om multiplikation som begrepp och dess egenskaper.

Fischbeins klassiker är intressant, för i introduktionen förklarar författarna att de har som hypotes att multiplikation som upprepad addition är en primitiv modell för barnen, dvs de antar att upprepad addition skulle vara något som eleverna liksom har med sig innan multiplikation formellt introduceras. I slutet av sin artikeln överger Fischbein och kollegor hypotesen om en primitiv modell och talar istället om multiplikation som upprepad addition som en didaktiskt modell. Alltså något som presenteras för barnen i en skolkontext. Det är ett mer rimligt synsätt. Visserligen vet man från kognitiv psykologi att redan nästan nyfödda barn har en slags uppfattning om addition. Och naturligtvis ligger idén om upprepad addition nära till hands, men det betyder ju inte att det är bra att fokusera på just den möjliga tolkningen av heltalsmultiplikation. Det finns faktiskt annan intuition hos barn. Det är t ex känt att bland de multiplikativa fenomenen så har de flesta barn före skolåldrarna idéer om uppdelning och linjäritet. Om jag ska köpa tre gånger så mycket godis behöver jag tre gånger så mycket pengar. Det är alltså läraren som bestämmer sig för att att låta den nyintroducerade termen multiplikation benämna just upprepad addition. Och det får konsekvenser.

Upprepad addition är en så starkt förankrad modell i våra läromedel att de flesta kanske inte ens kan tänka sig ett alternativ. Men så har det inte alltid varit. Ur Olas exemplar av Lärobok i Räknekonsten kan man läsa följande om vad multiplikation är:

Utdrag ur: P.J Pihlstrands Lärobok i Räknekonsten, från 1878

Att multiplicera ett tal med ett annat är att söka det tal i hvilket det första betraktadt som en enhet ingår till lika antal som 1 ingår i det andra.

Det här kanske låter lite intrikat, men ett intressant faktum är att den här definitionen inte alls använder sig av addition. Snarare utnyttjas ett slags proportionellt resonemang. Hur?

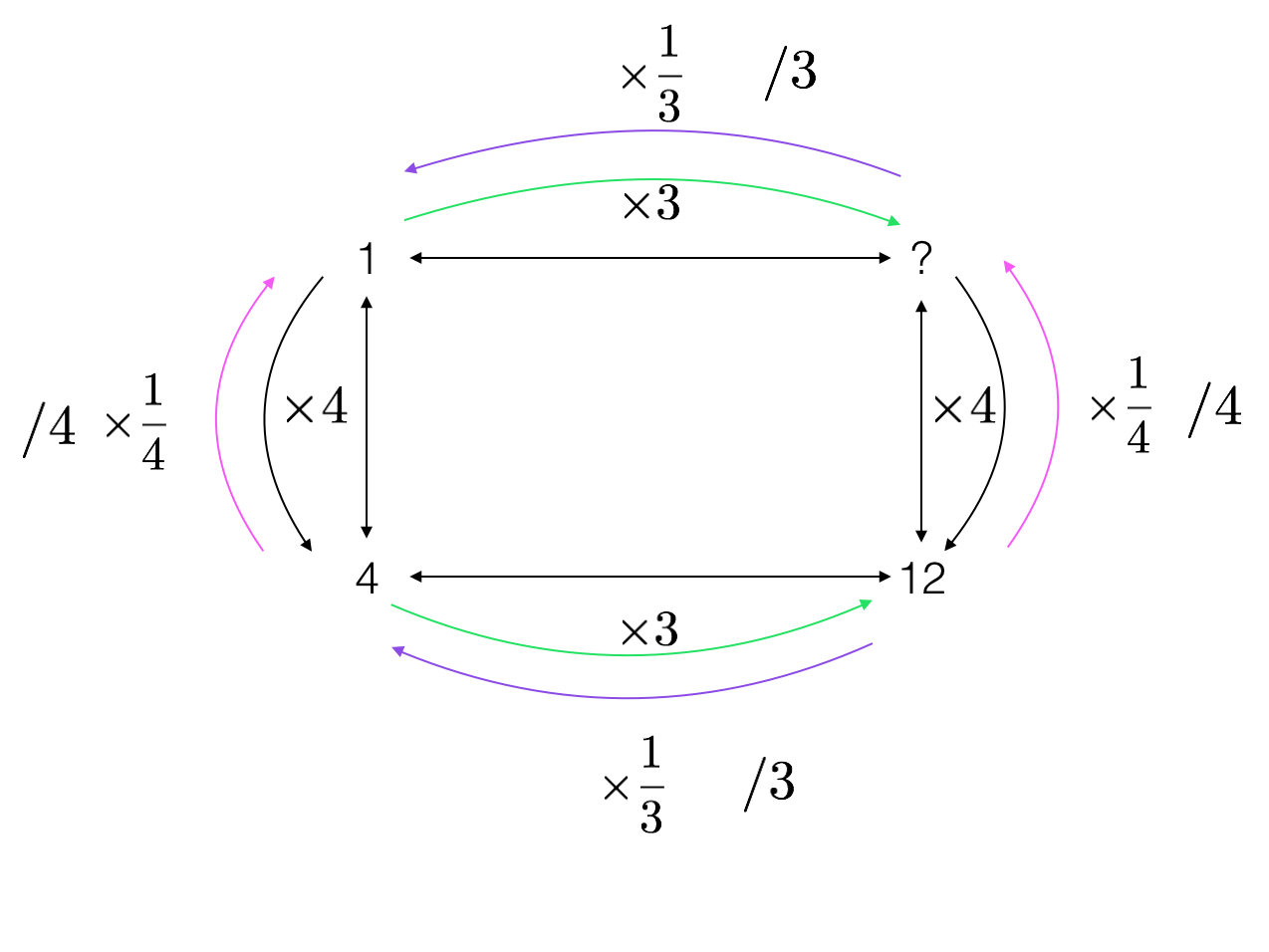
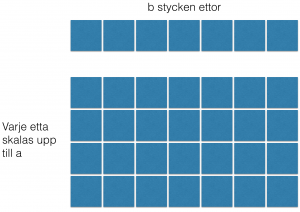
Vi söker ett c, dvs produkten. a \cdot b =c. Detta c ska ha egenskapen att a ingår i c som 1 ingår i b. Uttryckt som en proportion blir det a:c=1:b. Det vill säga, vi söker ett tal c vari det får plats lika mycket a som det får plats ettor i b. Med andra ord, om vi delar upp b i b stycken ettor, så kan vi sedan skala upp varje etta till a. Vi ritar:

På det här sätter återfår vi det som ibland kallas för area- eller rektangelmodellen för multiplikation. Med en sån här modell följer kommutativitet också omedelbart.

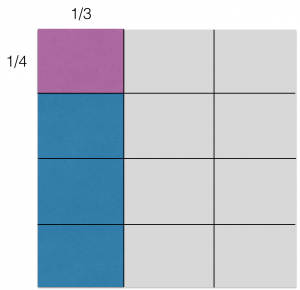
Den här modellen funkar faktiskt också för rationella tal. Om vi t ex ska multiplicera 1/4 med 1/3 så skalar vi bara det hela nedåt i horisontellt och vertikalt led.

Man kan visserligen förstå de oemotståndliga i att utgå från addition. All bra undervisning utgår från den lärandes tidigare kunskaper. Och elever i årskurs två är experter på addition. De förstår additiva fenomen till och med bättre än de flesta tror. När Ola och hans kollegor skulle utveckla ett test om additiva situationer så provades det ut i åk 2. Eleverna klarade nästan utan undantag allt. Av en slump testades även ett gäng ettor och även dessa visade upp en närmast perfekt förståelse för additiva situationer. Att lägga ihop och att lägga till, vilket är de enda två varianterna av addition som finns, har barn stora erfarenheter av redan innan de börjar skolan. Det som återstår är att till denna grundkunskap lägga till den matematiska formalism som gör att man kan hantera större tal och andra talområden.

Så är det ändå inte bra att bygga förståelsen för multiplikation på addition trots allt? Faktum är att multiplikation rent matematiskt definieras via addition. Hur, kanske du undrar. Det undrade Linda med:

Linda: Ola kan du definiera multiplikation?

Ola: Ja, med rekursion. m\cdot 0=0 och m\cdot (n+1)=m\cdot n+m . För naturliga tal, alltså. Man får läsa på om rekursionsprincipen för att förstå. Det är riktigt djupa grejjor

Linda: Men det här gäller ju bara för ickenegativa heltal. De andra talmängderna då? De är ju mycket mer intressanta. Det är ju för dem det blir problem med upprepad additions-modellen.

Ola: Man får utvidga operationerna när man utvidgar talmängderna. Rationella tal konstrueras t ex som par av heltal  (a,b) med b skilt från noll och där (a,b)=(c,d) om ad=bc. Symbolen (a,b) är naturligtvis vad vi normalt tänker på som a/b. Sedan definierar man multiplikation av sådana par som (a,b)\cdot(c,d)=(ac,bd). Dvs den räkneregel man förväntar sig (det är krångligare att definiera addition). Man får sedan bevisa att denna funktion är väldefinierad och att den har de egenskaper man förväntar sig.

Linda: Vad säger du nu egentligen? Att multiplikation av bråk är upprepad addition av täljaren och nämnaren var för sig när vi arbetar med rationella tal? Det ger ju ingen mening om vi ska betrakta bråk som tal. Det här känns som en efterhandskonstruktion. Vad är förresten ens addition om man ska vara petig med definitionen?

Ola: Att det är praktiskt att definiera multiplikation som upprepad addition med hjälp av rekursionsprincipen säger inte att det är ett särskilt bra sätt att tänka på multiplikation. I själva verket definieras addition som upprepad efterföljare Man utgår från att varje tal n har en efterföljare E(n). Sedan använder man rekursion och säger att n+0=n, n+(m+1)=E(n+m). Det är alltså ungefär lika krångligt att definiera addition som multiplikation om man ska göra det strikt. Att enbart tänka på multiplikation som upprepad addition är lika opraktiskt som att enbart tänka på addition som upprepad efterföljare.

Linda: Men hur blir det med kommutativiteten då? Det här verkar inte ens kommutativt, varken för addition eller multiplikation?

Ola: Nej, definitionerna är inte symmetriska. Både för addition och multiplikation för man helt enkelt bevisa att operationerna är kommutativa. Det kräver i sig en djup egenskap hos rekursion, nämligen att rekursivt definierade funktioner är entydiga. Med hjälp av det kan man bevisa kommutativitet för naturliga tal, sedan får man bevisa att det fortsätter gälla när man utvidgar till de hela talen, till de rationella och till de reella. Det blir ett par sidor med bevis. Det passar bra på en doktorandkurs i abstrakt algebra.

Linda: Men det här verkar ju jättekrångligt. Den här definitionen hjälper ju inte alls förståelsen av multiplikation. Jag tror ändå att jag stannar vid att förstå multiplikation som skalning. Jag kan inte heller minnas att jag har sett de här bevisen under min utbildning. Det känns onekligen lite bristfälligt att som matematiklärare och doktorand i matematikdidaktik inte matematiskt kunna bevisa vad addition och multiplikation är.

Ola: Nej, det är typiskt inget man gör i skolen eller ens i de inledande kurserna på högskolan. Det är matematiskt intressant, faktiskt nödvändigt, att veta att operationerna står på solid grund och att man kan definiera dem från mer grundläggande begrepp och bevisa att de har de egenskaper vi förväntar oss. Men det skapar i sig ingen ytterligare förståelse för additiva och multiplikativa fenomen.

Linda: Ingen tänker ju på addition som upprepad efterföljning, utom möjligen Allan Tarp, som envist framhärdar att barn bara ska räkna och inte addera.

Ola: Nej exakt. Iochförsig är det ju den egenskapen vi använder när vi hoppar fem steg till höger på tallinjen för att ta reda på vad n+5 är. Och på samma sätt är n*5 fem stycken n-hopp. Det är en användbara modeller och dessa tankesätt är viktiga komponenter av additivt respektive multiplikativt tänkande. Men de räcker ju inte ensamma till för att skapa en utvecklingsbar intuition om de olika operationerna. Om man tvingade elever att förstå addition enbart som upprepad efterföljare skulle de bli matematiskt handikappade. Det är just det som händer när man lurar dem att se multiplikation som upprepad addition.

Linda: Det är matematisk möjligt men psykologiskt tarvligt.

Här har vi nog kommit till essensen i vår diskussion. Det tycks vara pedagogisk attraktivt att inledningsvis låta multiplikation vara upprepad addition och det är inte matematisk fel. Additivt tänkande är en del av multiplikativt tänkande, precis som efterföljare är en del av additivt tänkande.

Nej, det verkar faktiskt inte så. Likt nykläckta kycklingar som präglas direkt på mamman och sedan inte viker från hennes sida, så präglas barnen till modellen multiplikation som upprepad addition och viker sedan inte från additionens sida. Vill vi verkligen det? Nej det vill vi inte. Och ni borde inte vilja heller, faktiskt.

Om ni fortfarande tror att det är en bra idé, så finns det gott om andra forskare som är redo att medelst sina forskningsresultat övertyga er om motsatsen. Så för de som fortfarande planerar att föra eleverna bakom ljuset någon gång runt Halloween i  årskurs 2 rekommenderar vi läsning av: Dooren et. al, 2010; Greer, 1994; Nesher, 1988; Nunes & Bryant, 1996; Piaget, Grize, Szeminska, & Bangh, 1977; Squire, Davies, & Bryant, 2004; Vamvakoussi et. al 2013. För att bara nämna några.

 

Referenser

Dooren, W. V., Bock, D. D., & Verschaffel, L. (2010). From addition to multiplication… and back: The development of students’ additive and multiplicative reasoning skills. Cognition and Instruction, 28(3), 360-381.

Greer, B. (1994). Extending the meaning of multiplication and division. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 61–85). Albany: State, University of New York Press.

Nesher, P. (1988). Multiplicative school word problems: Theoretical approaches and empirical findings. In J. Hiebert & M. Behr (Eds.), Number concepts and operations in the middle grades (Vol. 2, pp. 19–40). Reston, VA: National Council of Teachers of Mathematics.

Nunes, T., & Bryant, P. (1996). Children doing mathematics. Oxford: Wiley.

Piaget, J., Grize, J., Szeminska, A., & Bang, V. (1977). Epistemology and psychology of functions (F. Castelanos & V. Anderson, Trans.). Dordrecht, The Netherlands: Reidel.

Squire, S., Davies, C., & Bryant, P. (2005). Does the cue help? Children’s understanding of multiplicative concepts in different problem contexts. British Journal of Educational Psychology, 74, 515–32.

Vamvakoussi, X., Van Dooren, W., & Verschaffel, L. (2013). Brief Report. Educated adults are still affected by intuitions about the effect of arithmetical operations: evidence from a reaction-time study. Educational Studies in Mathematics, 82(2), 323-330.

När Ola träffade Linda på en kompetensutveckling, som Ola anordnade och Linda deltog i, tänkte han: Det där är ingen vanlig lärarinna! Kanske var det fårpälsvästen, kanske var det påståendet att hennes elever minsann glatt läste populärvetenskapliga böcker om matematik helt frivilligt. Men mest troligt är att det var hennes tröttsamma framhärdande att proportionella resonemang är det viktigaste i hela grundskolan. Typiskt att folk tycker att just deras grejer är så himla intressanta, tänkte Ola och kategoriserade Linda som en galen proportionalitetskvinna. Men hon var rolig och snabbtänkt och väldigt entusiastisk, så det var värt att ta reda på lite mer om Lindas övertygelser. Efter lite samtal drog sig Ola till minnes en artikel han reviewade något år tidigare. Författaren insisterade på att proportionalitet minsann var det viktigaste begreppet i hela skolmatematiken. Hmm, sådär skriver alla om sina favoritbegrepp, tänkte Ola även då, och refuserade det hela. Var det möjligen samma galna proportionalitetskvinna? Ja, visade det sig.  (Artikeln är numera publicerad så allt är förlåtet.)

Men trägen vinner. Ni som läste vår senaste bloggpost har kanske redan anat att Ola är omvänd. Och på Biennalen i Karlstad för några veckor sedan stod Ola glatt och föreläste om proportionalitetsbegreppets förträfflighet. Två gånger till och med! För förskoleklass till sexan och för sjuan till gymnasiet. Båda gångerna tillsammans med Linda, som nu helt har frälst Ola som numera får betraktas som en fullfjädrad proportionalitets-förespråkare.

Vad är då en proportion? För att förklara det måste vi först förstå begreppet förhållande. Det går som bekant inte att förklara något begrepp utan förståelse för andra begrepp. Ett förhållande är en multiplikativ relation mellan två kvantiteter (eller två saker som Ola brukar säga, oprecis som han är). Ett sätt att uttrycka ett förhållande är \frac{a}{b}. Som ett bråk. En proportion är en likhet mellan två förhållanden. \frac{a}{b}=\frac{c}{d}. Men när vi betraktar proportioner är vi inte nödvändigtvis ute efter att beräkna kvoten hos dessa två bråk, utan fokuserar på just det faktum att de två förhållandena är lika.

Proportionella resonemang kan introduceras minst lika tidigt som man introducerar multiplikation. Betrakta följande: 

 

Ur äppelrelationen kan man dra slutsatsen att Stora Björn har 3 ggr så mycket av allt (gröna pilen). Men det följer också att eftersom Lilla björn har 4 ggr så många äpplen som apelsiner så måste detta även gäller för Stora björn (svarta pilarna). Drar vi alla dylika resonemang till sin spets och även (i enlighet med en av våra tidigare bloggposter) beaktar inverser kan vi schematisera det hela så här:

Notera speciellt att man kan tänka på inversen till multiplikation med 3 på två sätt: division med 3 eller multiplikation med ⅓. Man får massor med olika möjligheter att räkna ut vilket tal som ska stå på frågetecknets plats. Och den typ av resonemang som man för är helt oberoende av överväganden som har med den ursprungliga situationens konkreta gestaltning att göra. Det är bara det faktum att det handlar om ett proportionellt resonemang som spelar roll. Och egentligen finns förstås alla dessa relationer redan i representationen

\frac{1}{4}=\frac{?}{12}

Det är just det här som gör proportionella resonemang så förträffliga. Om eleverna lär sig att identifiera situationer där två förhållanden är lika och resonera om de inbördes multiplikativa relationerna så behöver de inte nöta in en herrans massa olika situationer i olika områden år ut och år in. Vad pratar vi om egentligen? Jo att skala upp och ner bråk, beräkna skala, procent, likformighet, sammansatta enheter som hastighet, densitet och kilopris, likformighet inom geometrin, likformig sannolikhet och alla uppgifter som illustrerar ett multiplikativt samband där tre värden är givna och det fjärde saknas beräknas enklast med just proportionella resonemang. Alla dessa funktioner som kan beskrivas som en proportionalitet f(x)=kx, U=RI, s=vt, O=\pi d…

Eleverna kan lätt få en känsla av att matematiska situationer från olika delar av skolmatematiken är fundamentalt olika, men så är det ju inte. Det är en stor befrielse för eleverna att inse att samma resonemang fungerar inom alla möjliga områden. Matematiken krymper och det är möjligt att göra en syntes på grund av denna  matematiska ide dyker upp om och om igen, inom en mängd olika områden. Titta på uppgifterna nedan. De är alla hämtade från olika kapitel i en och samma textbok för … ja fundera på när eleverna arbetar med den här matematiken och gissa?

Vikterna mellan två paket förhåller sig som 2:5. Om det ena paketet väger 10 kg, vad kan då det andra paketet väga?

Jannes hår växer 17 µm per timme. Hur lång tid tar det för hans hår att växa 4 cm?

Lös ekvationen:\frac{18}{6x}=\frac{9}{3}

Hur stor diameter har en cirkel med omkretsen 35 cm?

En skobutik säljer sina skor för 160 % av inköpspriset. Vad är inköpspriset för ett par skor som kostar 760 kr?

Fem meter rep kostar 150 kr. Vad kostar tjugo meter rep?

Under en dag gör en maskin 5900 lampor. Vid en kontroll visar det sig att 26 av dem är felaktiga. Ungefär hur många trasiga lampor borde det finnas vid en leverans av 2000 lampor?

Till 5 liter vit färg krävs det 7 droppar pigment för att färgen ska bli ljusblå. Hur många droppar pigment går det åt till 12 liter färg?

En 22 cm lång kändisdocka är tillverkad i skala 1:8. Hur lång var personen som stod modell för dockan?

En kon med höjden 16 cm har en volym på 54 cm³. Hur stor volym har en (likformig) kon med höjden 8 cm?

[Den här är något mer intrikat då eleverna behöver identifiera att radien är proportionell mot höjden och samtidigt hålla reda på att areaskalan är längdskalan i kvadrat. En lösning baserad på proportionella resonemang presenteras sist i inlägget.]

Lindas elever i Kriminalvården får träna på att identifiera om det finns ett proportionellt samband i spel i de uppgifter de ska lösa. De är ju vuxna nu och för de allra flesta har det gått sisådär med skolmatematiken, av olika anledningar. Påfallande många tycker ända att det är konstigt att ingen har gjort sig besväret att upplysa dem om att samma resonemang är tillämpligt på så många olika situationer. Det hade ju varit så mycket enklare då, att hålla reda på allt. Det är ju inte konstigt att de misstänker att de har blivit utsatta för en konspiration med syftet att får dem att känna sig korkade helt i onödan!

Ta det här med procent till exempel. Varje år sedan årskurs 5 har eleverna nött igenom ett kapitel om procent. Procent, procent, procent, procent, procent, procent. Ständigt dessa procent. Som om det skulle behövas särskild träning för att hantera ett proportionellt multiplikativt samband där vi utgår från en helheten 100?

Höjning med 20%:  \frac{600kr}{100\%}=\frac{?}{120\%}

Sänkning med 30%:  \frac{600kr}{100\%}=\frac{?}{70\%}

Eller kanske vad motsvarar delen 30 % i pengar? \frac{600kr}{100\%}=\frac{?}{30\%}

Det coola med det här tankesättet är att det egentligen inte spelar någon roll vad man sätter som täljare och nämnare, bara man är konsekvent. Det är enbart den multiplikativa relationen som spelar roll.

Problemet är kanske att procent ofta undervisas som en additiv situation där eleverna först ska räkna ut sänkningen, eller höjningen, och sen lägga till eller dra ifrån. Helt onödigt om du frågar oss. Varför inte bara servera definitionen från 1878 års ”Lärobok i Räknekonsten” av P.J. Pihlstrand. Regula de tri är en beräkningsteknik för proportionalitet, kan man säga.

Det är allt.

Kanske tycker en del att vårt resonemang verkar lite esoteriskt och abstrakt och att det inte skulle gynna förståelsen. Men de har fel. Såväl lata och ointresserade elever som genuint intresserade attraheras av tanken att attackera uppgifter från diverse områden med samma verktyg. (Observera att det inte ligger någon värdering i begreppet lat och ointresserad. Linda är rätt lat själv och att hata matematik måste betraktas som en mänsklig rättighet.) Att resonera proportionellt är inte en algoritm som kan tillämpas utan att ha sorterat informationen i uppgifterna. Som elev måste du fundera på vad som förhåller sig proportionellt till vad innan hen kan beskriva proportionen i symboler. Om inte det är bra matematiskt tänkande, då vet vi inte vad vi ska ägna oss år på lektionerna.

Här är vårt bästa tips! Hylla likhetstecknets betydelse, som är helt centralt för de proportionella resonemangen. Arbeta för att etablera en sociomatematisk norm som innebär att närhelst proportionella resonemang är tillämpliga så är det den sortens resonemang som smäller högst när det gäller att delta i klassrumsdiskursen. Då kan du krympa matematiken och bryta dig loss från oppgavediskursen. När färre uppgifter behöver räknas frigörs tid för både elever och lärare att fördjupa sina betraktelser över vad det är för sorts matematiska ideer vi arbetar med. Du och dina elever slipper också att tröska igenom ett snarlikt procentkapitel från årskurs 5 till kurs 1 på gymnasiet och bäst av allt: Dina elever får ett verktyg som hjälper den att både förstå och hantera stora delar av skolmatematiken.

Det finns mycket mer att säga om det här… men eftersom våra bloggposter tenderar att likna romaner så slutar vi här. Vi hade som mål att den här skulle bli rätt kort. Se hur det gick med den saken:-) Om du vill läsa mer så rekommenderar vi vår artikelserie om proportionella resonemang i Nämnaren nr 2,3 och 4 2017 och nr 1 2018.

P.S. För de som tycker att vi verkar vara galna proportionalitets-människor så kan vi beta med att vi räknade igenom ett NP för årskurs 9 och konstaterade att 70% av uppgifterna kunde lösas med resonemang om förhållanden och proportioner.

Angående konens volym: Eftersom höjden är proportionell mot radien så kommer radien i den mindre konen vara halva radien i förhållande till den stora. Eleverna behöver också inse att \pi/3 är en konstant i volymberäkningen.

\frac{54cm^3}{r^2\cdot 16cm}=\frac{?}{((1/2)r)^2\cdot 8cm}

En halv i kvadrat är en fjärdedel och radien annulleras vilket betyder att den nya relationen i volymberäkningen är 1/4 \cdot 8=2. De som har arbetat med skalning mellan längd, area och volym inser detta helt utan beräkningar och kan genast sätta upp nedanstående proportion:-)

\frac{54}{16}=\frac{?}{2}

dvs V=54/8=6.25 kubikcentimeter. 

 

Linda Marie Ahl & Ola Helenius

Har du någon gång gjort något som du skulle vilja ha ogjort? Det går ju inte. Men i matematiken går det ibland. Med det förträffliga fenomenet invers. En magisk ogörningsoperator. Vad vore matematiken utan invers? I bästa fall hälften av vad den nu är, men troligen inte ens det. Vad skulle vi göra utan inversen till addition (subtraktion), inversen till multiplikation, (division) och inversen till exponentiering (logaritmering)? För att inte tala om den multiplikativa inversen till ett tal, det vill säga det tal som multiplicerat med originaltalet ger det neutrala elementet 1.
Eller den additiva inversen för den delen, det som adderat till talet ger additionens neutrala element 0. Och hur ska vi dividera rationella tal utan invers? Eller lösa ekvationer? Nej, matematiken vore inte mycket utan det centralaste centrala begreppet: invers.
Läs vidare …