Upprepad addition är en vanlig modell för multiplikation. Det är den modell som sedan 1786 sämst har klarat sin uppgift. Eller ja, det där drog vi ju bara till med för att hamna i gott akademiskt sällskap. I själva verket vet vi inte om det på den tiden fanns någon sämre modell. Men om ni läser vidare ska ni få se en bättre från 1878.
Vi menar att multiplikation och dess egenskaper missrepresenteras med modellen upprepad addition. Multiplikationen som fenomen och dess egenskaper behandlas lättvindigt med tanke på hur stor del av den obligatoriska skolans matematik som faktiskt handlar om multiplikativa strukturer och proportionella resonemang. Vi ska argumentera för att vi borde sluta upp med det här.
Upprepad addition är en modell för multiplikation som bara gäller för naturliga tal. Med den här modellen är det t ex en helt självklar sanning all multiplikation alltid gör större (eller lika om man multiplicerar med ett). Den här uppfattningen får vi sedan ägna resten av elevernas skolgång till att försöka ta ur dem. Senast igår ställde den till problem när en av Lindas (vuxna) studenter skulle beräkna hur många frön man måste så för att få 20 livsdugliga solrosor, om grobarheten är 83%. Han hade nedtecknat en divisionsprocedur, men sedan stannade han upp i sin beräkning. Linda såg att han tvekade. -Vad är det som stör dig, frågade Linda? -Ja, det känns ju helt fel att dividera när jag vill att det ska bli fler frön… Han tyckte alltså att det var direkt obehagligt att behöva dividera med 0.85. Han lider helt klart av multiplikation som upprepad addition-villfarelsen: Division gör mindre, multiplikation gör större.
Upprepad addition är en oduglig modell för att illustrera den viktiga egenskapen kommutativitet. Att 2+2+2 är lika 3+3 kan vi ju se för att båda är lika med 6. Lika lätt är det i varje konkret fall. Men hur blir det i det allmänna fallet? Varför är a stycken b lika med b stycken a? Fundera på det du. Och hur fungerar additionsmodellen för 1/2\cdot3/5? Inte alls bra, eller hur.
Mängden forskning som påvisar problem med “multiplikation som upprepad addition” är omfattande. Ett aktuellt svenskt exempel är t ex Kerstin Larssons avhandling från 2017 och ett mer klassisk exempel är Fischbein och kollegors studie från 1985. I båda fallen visas att den additionsbaserade modellen leder till problem för elevernas uppfattning om multiplikation som begrepp och dess egenskaper.
Fischbeins klassiker är intressant, för i introduktionen förklarar författarna att de har som hypotes att multiplikation som upprepad addition är en primitiv modell för barnen, dvs de antar att upprepad addition skulle vara något som eleverna liksom har med sig innan multiplikation formellt introduceras. I slutet av sin artikeln överger Fischbein och kollegor hypotesen om en primitiv modell och talar istället om multiplikation som upprepad addition som en didaktiskt modell. Alltså något som presenteras för barnen i en skolkontext. Det är ett mer rimligt synsätt. Visserligen vet man från kognitiv psykologi att redan nästan nyfödda barn har en slags uppfattning om addition. Och naturligtvis ligger idén om upprepad addition nära till hands, men det betyder ju inte att det är bra att fokusera på just den möjliga tolkningen av heltalsmultiplikation. Det finns faktiskt annan intuition hos barn. Det är t ex känt att bland de multiplikativa fenomenen så har de flesta barn före skolåldrarna idéer om uppdelning och linjäritet. Om jag ska köpa tre gånger så mycket godis behöver jag tre gånger så mycket pengar. Det är alltså läraren som bestämmer sig för att att låta den nyintroducerade termen multiplikation benämna just upprepad addition. Och det får konsekvenser.
Upprepad addition är en så starkt förankrad modell i våra läromedel att de flesta kanske inte ens kan tänka sig ett alternativ. Men så har det inte alltid varit. Ur Olas exemplar av Lärobok i Räknekonsten kan man läsa följande om vad multiplikation är:
Utdrag ur: P.J Pihlstrands Lärobok i Räknekonsten, från 1878
Att multiplicera ett tal med ett annat är att söka det tal i hvilket det första betraktadt som en enhet ingår till lika antal som 1 ingår i det andra.
Det här kanske låter lite intrikat, men ett intressant faktum är att den här definitionen inte alls använder sig av addition. Snarare utnyttjas ett slags proportionellt resonemang. Hur?
Vi söker ett c, dvs produkten. a \cdot b =c. Detta c ska ha egenskapen att a ingår i c som 1 ingår i b. Uttryckt som en proportion blir det a:c=1:b. Det vill säga, vi söker ett tal c vari det får plats lika mycket a som det får plats ettor i b. Med andra ord, om vi delar upp b i b stycken ettor, så kan vi sedan skala upp varje etta till a. Vi ritar:
På det här sätter återfår vi det som ibland kallas för area- eller rektangelmodellen för multiplikation. Med en sån här modell följer kommutativitet också omedelbart.
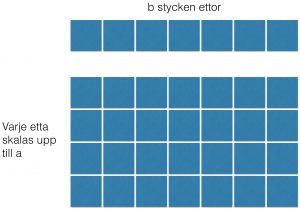
Den här modellen funkar faktiskt också för rationella tal. Om vi t ex ska multiplicera 1/4 med 1/3 så skalar vi bara det hela nedåt i horisontellt och vertikalt led.

Man kan visserligen förstå de oemotståndliga i att utgå från addition. All bra undervisning utgår från den lärandes tidigare kunskaper. Och elever i årskurs två är experter på addition. De förstår additiva fenomen till och med bättre än de flesta tror. När Ola och hans kollegor skulle utveckla ett test om additiva situationer så provades det ut i åk 2. Eleverna klarade nästan utan undantag allt. Av en slump testades även ett gäng ettor och även dessa visade upp en närmast perfekt förståelse för additiva situationer. Att lägga ihop och att lägga till, vilket är de enda två varianterna av addition som finns, har barn stora erfarenheter av redan innan de börjar skolan. Det som återstår är att till denna grundkunskap lägga till den matematiska formalism som gör att man kan hantera större tal och andra talområden.
Så är det ändå inte bra att bygga förståelsen för multiplikation på addition trots allt? Faktum är att multiplikation rent matematiskt definieras via addition. Hur, kanske du undrar. Det undrade Linda med:
Linda: Ola kan du definiera multiplikation?
Ola: Ja, med rekursion. m\cdot 0=0 och m\cdot (n+1)=m\cdot n+m . För naturliga tal, alltså. Man får läsa på om rekursionsprincipen för att förstå. Det är riktigt djupa grejjor
Linda: Men det här gäller ju bara för ickenegativa heltal. De andra talmängderna då? De är ju mycket mer intressanta. Det är ju för dem det blir problem med upprepad additions-modellen.
Ola: Man får utvidga operationerna när man utvidgar talmängderna. Rationella tal konstrueras t ex som par av heltal (a,b) med b skilt från noll och där (a,b)=(c,d) om ad=bc. Symbolen (a,b) är naturligtvis vad vi normalt tänker på som a/b. Sedan definierar man multiplikation av sådana par som (a,b)\cdot(c,d)=(ac,bd). Dvs den räkneregel man förväntar sig (det är krångligare att definiera addition). Man får sedan bevisa att denna funktion är väldefinierad och att den har de egenskaper man förväntar sig.
Linda: Vad säger du nu egentligen? Att multiplikation av bråk är upprepad addition av täljaren och nämnaren var för sig när vi arbetar med rationella tal? Det ger ju ingen mening om vi ska betrakta bråk som tal. Det här känns som en efterhandskonstruktion. Vad är förresten ens addition om man ska vara petig med definitionen?
Ola: Att det är praktiskt att definiera multiplikation som upprepad addition med hjälp av rekursionsprincipen säger inte att det är ett särskilt bra sätt att tänka på multiplikation. I själva verket definieras addition som upprepad efterföljare Man utgår från att varje tal n har en efterföljare E(n). Sedan använder man rekursion och säger att n+0=n, n+(m+1)=E(n+m). Det är alltså ungefär lika krångligt att definiera addition som multiplikation om man ska göra det strikt. Att enbart tänka på multiplikation som upprepad addition är lika opraktiskt som att enbart tänka på addition som upprepad efterföljare.
Linda: Men hur blir det med kommutativiteten då? Det här verkar inte ens kommutativt, varken för addition eller multiplikation?
Ola: Nej, definitionerna är inte symmetriska. Både för addition och multiplikation för man helt enkelt bevisa att operationerna är kommutativa. Det kräver i sig en djup egenskap hos rekursion, nämligen att rekursivt definierade funktioner är entydiga. Med hjälp av det kan man bevisa kommutativitet för naturliga tal, sedan får man bevisa att det fortsätter gälla när man utvidgar till de hela talen, till de rationella och till de reella. Det blir ett par sidor med bevis. Det passar bra på en doktorandkurs i abstrakt algebra.
Linda: Men det här verkar ju jättekrångligt. Den här definitionen hjälper ju inte alls förståelsen av multiplikation. Jag tror ändå att jag stannar vid att förstå multiplikation som skalning. Jag kan inte heller minnas att jag har sett de här bevisen under min utbildning. Det känns onekligen lite bristfälligt att som matematiklärare och doktorand i matematikdidaktik inte matematiskt kunna bevisa vad addition och multiplikation är.
Ola: Nej, det är typiskt inget man gör i skolen eller ens i de inledande kurserna på högskolan. Det är matematiskt intressant, faktiskt nödvändigt, att veta att operationerna står på solid grund och att man kan definiera dem från mer grundläggande begrepp och bevisa att de har de egenskaper vi förväntar oss. Men det skapar i sig ingen ytterligare förståelse för additiva och multiplikativa fenomen.
Linda: Ingen tänker ju på addition som upprepad efterföljning, utom möjligen Allan Tarp, som envist framhärdar att barn bara ska räkna och inte addera.
Ola: Nej exakt. Iochförsig är det ju den egenskapen vi använder när vi hoppar fem steg till höger på tallinjen för att ta reda på vad n+5 är. Och på samma sätt är n*5 fem stycken n-hopp. Det är en användbara modeller och dessa tankesätt är viktiga komponenter av additivt respektive multiplikativt tänkande. Men de räcker ju inte ensamma till för att skapa en utvecklingsbar intuition om de olika operationerna. Om man tvingade elever att förstå addition enbart som upprepad efterföljare skulle de bli matematiskt handikappade. Det är just det som händer när man lurar dem att se multiplikation som upprepad addition.
Linda: Det är matematisk möjligt men psykologiskt tarvligt.
Här har vi nog kommit till essensen i vår diskussion. Det tycks vara pedagogisk attraktivt att inledningsvis låta multiplikation vara upprepad addition och det är inte matematisk fel. Additivt tänkande är en del av multiplikativt tänkande, precis som efterföljare är en del av additivt tänkande.
Nej, det verkar faktiskt inte så. Likt nykläckta kycklingar som präglas direkt på mamman och sedan inte viker från hennes sida, så präglas barnen till modellen multiplikation som upprepad addition och viker sedan inte från additionens sida. Vill vi verkligen det? Nej det vill vi inte. Och ni borde inte vilja heller, faktiskt.
Om ni fortfarande tror att det är en bra idé, så finns det gott om andra forskare som är redo att medelst sina forskningsresultat övertyga er om motsatsen. Så för de som fortfarande planerar att föra eleverna bakom ljuset någon gång runt Halloween i årskurs 2 rekommenderar vi läsning av: Dooren et. al, 2010; Greer, 1994; Nesher, 1988; Nunes & Bryant, 1996; Piaget, Grize, Szeminska, & Bangh, 1977; Squire, Davies, & Bryant, 2004; Vamvakoussi et. al 2013. För att bara nämna några.
Referenser
Dooren, W. V., Bock, D. D., & Verschaffel, L. (2010). From addition to multiplication… and back: The development of students’ additive and multiplicative reasoning skills. Cognition and Instruction, 28(3), 360-381.
Greer, B. (1994). Extending the meaning of multiplication and division. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 61–85). Albany: State, University of New York Press.
Nesher, P. (1988). Multiplicative school word problems: Theoretical approaches and empirical findings. In J. Hiebert & M. Behr (Eds.), Number concepts and operations in the middle grades (Vol. 2, pp. 19–40). Reston, VA: National Council of Teachers of Mathematics.
Nunes, T., & Bryant, P. (1996). Children doing mathematics. Oxford: Wiley.
Piaget, J., Grize, J., Szeminska, A., & Bang, V. (1977). Epistemology and psychology of functions (F. Castelanos & V. Anderson, Trans.). Dordrecht, The Netherlands: Reidel.
Squire, S., Davies, C., & Bryant, P. (2005). Does the cue help? Children’s understanding of multiplicative concepts in different problem contexts. British Journal of Educational Psychology, 74, 515–32.
Vamvakoussi, X., Van Dooren, W., & Verschaffel, L. (2013). Brief Report. Educated adults are still affected by intuitions about the effect of arithmetical operations: evidence from a reaction-time study. Educational Studies in Mathematics, 82(2), 323-330.

Ännu inga kommentarer. Kommentera gärna!